Thermal Conduction, Thermal Conductivity – Problems and Solutions – Laman 3

03. A cylindrical rod has a temperature gradient of -0,5 K m^-1 . The rate of heat flow in to P is 50 J s^-1 .

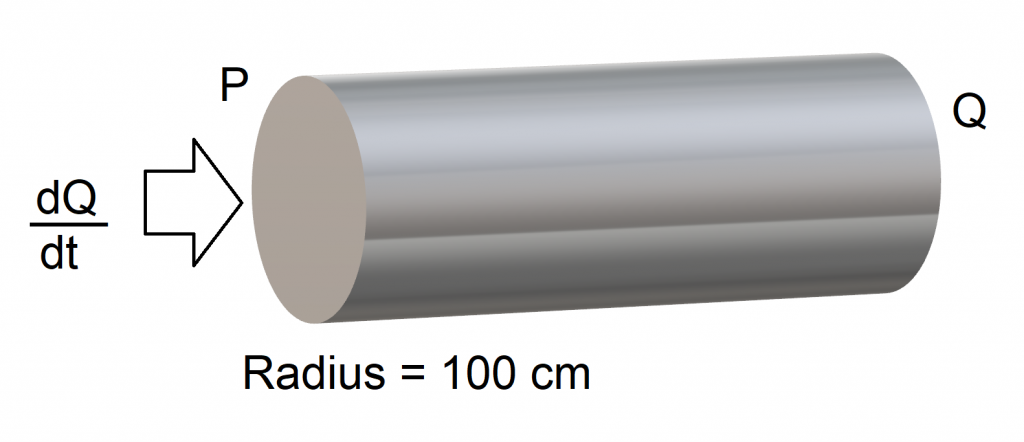
Assuming that heat cannot escape through the curved surface of the solid but only through its cross section, calculate the thermal conductivity of the rod.

$\frac {dQ}{dt}= 50 J s^{-1} \\ \\ \frac{d\theta}{dx}= - 0,5 K m^{-1}$

Area of cross section, $A = \pi (1)^2 m^2 = 3,142 m^2 \\ \\$

Quick Note !

The rate of heat flow $\frac {dQ}{dt}$ perpendicular to the cross-sectional area A depends on :

the cross-sectional A.

the temperature gradient $-\frac {d\theta}{dt}$ .

the material of the solid.

It is found that

$\frac { dQ }{ dt } \propto \quad A\\ \\ \frac { dQ }{ dt } \propto -\frac { d\theta }{ dx } \\ \\$
Therefore

$\frac { dQ }{ dt } \propto -A\frac { d\theta }{ dx } \\ \\ \\ \\$
Where k = thermal conductivity of material.
Therefore, thermal conductivity k is defined as the negative rate of heat flow per unit area perpendicular to the flow per unit temperature gradient. Metals, being good conductors, have higher value of k compare to non-metals. For same metals, k decreases slightly as the temperature increases. However, the decrease is mostly negligible.

Solution

$\\ \\ \frac { dQ }{ dt } =-kA\frac { d\theta }{ dx } \\ \\ k=\frac { -\frac { dQ }{ dt } }{ A\frac { d\theta }{ dx } } \\ \\ k\quad =\quad \frac { -50 }{ 3,142\quad (-0,5) } W\quad { m }^{ -1 }{ K }^{ -1 }\\ \\ k\quad =\quad 31,8\quad W\quad { m }^{ -1 }{ K }^{ -1 }\\ \\$