Thermal Conduction, Thermal Conductivity – Problems and Solutions – Laman 6

06. A Composite rod of diameter 16 mm is insulated as show in the figure.

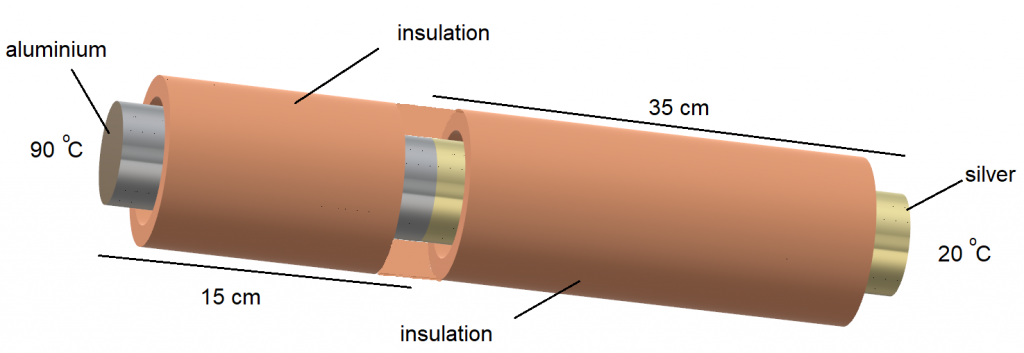
Calculate :

a. the thermal resistance of the aluminium rod and silver rod respectively
b. the temperature at the interface
c. the rate of heat flow through the composite rod.
— Thermal conductivities of aluminium and silver are 201 W m^-1K^-1 and 419 W m^-1 K^-1 respectively.–

Solution

a. $R_\theta$ of Aluminium
${ R }_{ \theta }\quad aluminium\quad =\frac { { l }_{ A } }{ { k }_{ A }A } \\ \\ { R }_{ \theta }\quad aluminium\quad =\frac { 0.15 }{ 201\pi \frac { ({ 16\quad x\quad { 10 }^{ -3 } })^{ 2 } }{ 4 } } K{ W }^{ -1 }\\ \\ { R }_{ \theta }\quad aluminium\quad =3.71\quad K{ W }^{ -1 }$

$R_\theta$ of Silver
${ R }_{ \theta }\quad aluminium\quad =\frac { { l }_{ A } }{ { k }_{ A }A } \\ \\ { R }_{ \theta }\quad aluminium\quad =\frac { 0.35 }{ 419\pi \frac { ({ 16\quad x\quad { 10 }^{ -3 } })^{ 2 } }{ 4 } } K{ W }^{ -1 }\\ \\ { R }_{ \theta }\quad aluminium\quad =4.15\quad K{ W }^{ -1 }$

b. Temperature at the interface = $\theta$
$\theta \quad =\quad \left( \frac { \frac { { k }_{ A }{ \theta }_{ 1 } }{ { l }_{ A } } +\frac { { k }_{ S }{ \theta }_{ 2 } }{ { l }_{ S } } }{ \frac { { k }_{ A } }{ { l }_{ A } } +\frac { { k }_{ S } }{ { l }_{ S } } } \right) \\ \\ \theta \quad =\quad \left( \frac { \frac { 201\quad x\quad 90 }{ 0.15 } +\frac { 419\quad x\quad 20 }{ 0.35 } }{ \frac { 201 }{ 0.15 } +\frac { 419 }{ 0.35 } } \right) \quad _{ }^{ 0 }{ C }\\ \\ \theta \quad ={ 57 }^{ o }C$

c. the rate of heat flow through the composite rod.

$\frac { dQ }{ dt } =\frac { temperature\quad difference }{ total\quad thermal\quad resistance } \\ \\ \frac { dQ }{ dt } =\frac { 90\quad -\quad 20 }{ 3.71\quad +\quad 4.15 } W\\ \\ \frac { dQ }{ dt } =8.91\quad W$